Математики из МГУ совместно с иностранными специалистами заложили основы Нийенхейсовой геометрии – раздела математики, который тесно связан с интегрируемыми системами, алгеброй, дифференциальной геометрией и математической физикой. Работы (1 и 2), поддержанные грантом РНФ, можно найти на сайте arXiv.org, сейчас они готовятся к публикации в ведущих мировых математических журналах.
В основе современной физики лежит геометрия. Так, например, теория относительности Альберта Эйнштейна связана с псевдоримановой геометрией. В этой геометрии информация о геометрической структуре записывается в виде матрицы – заключенных в таблицу элементов объекта, который изучают математики. В такой таблице все элементы имеют два номера – номер строки, где он записан, и номер столбца. Так же, как в Экселе.
Компоненты, то есть значения элементов таблицы, меняются от точки к точке. Если размерность пространства, например, три (длина, ширина и высота), то размер такой матрицы 3 на 3, то есть у нее 9 параметров. На матрицу накладывается дополнительное условие – симметричность. Это значит, что элементы матрицы, симметричные относительно диагонали, одинаковы. Это значит, что количество параметров не 9, а 6. Свою теорию относительности Альберт Эйнштейн формулировал именно в терминах псевдоримановой геометрии – это ее математический инструментарий. Он объединил пространство и время, получив четырехмерный объект, поэтому матрица у него имеет размер 4 на 4. В свою очередь, уравнение Эйнштейна описывает гравитацию через компоненты матрицы. Именно его численно решают астрофизики, когда пытаются описать поведение физических объектов в окрестности черных дыр.
Другая геометрия, которую используют в классической механике и частично в квантовой, называется Пуассоновой геометрией. В ней вся геометрическая информация содержится в матрице, которая в этом случае не симметрична, а кососимметрична. Это означает, что на месте ij в этой матрице стоит та же функция, что и на ji, только взятая со знаком минус. На компоненты этой матрицы наложены дополнительные условия – система дифференциальных тождеств Якоби.
Пуассонова геометрия возникла сначала как инструмент в теории динамических систем. Сейчас ее используют, например, в теории деформационного квантования, за создание которой известный французский математик российского происхождения Максим Концевич получил премию Филдса и дважды премию Миллера (один раз – за физическую часть, другой раз – как раз за соответствующий математический инструментарий). Эта теория позволяет комплексно подходить к переходу от классической физики к квантовой. Сегодня в этом направлении множество вопросов, которые активно изучаются.
«В своих работах мы обратились к геометрии, где информация о структуре также содержится в матрице. Важное отличие в том, что это за матрица, — объясняет Андрей Коняев, кандидат физико-математических наук, доцент кафедры дифференциальной геометрии мехмата МГУ имени М.В. Ломоносова. — Традиционно матрицами в математике записывают три разных объекта – билинейная форма, 2-вектор и оператор. Матрицами их записывают потому, что эти объекты называются тензорами и правильно преобразуются при замене координат. В псевдоримановой геометрии фигурируют билинейная форма, в пуассоновой – 2-вектор, а в новой геометрии, которая получила название Нийенхейсовой, речь про операторы».
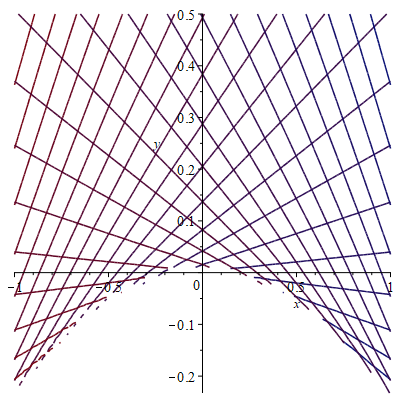
Представьте себе обычную материю: кусочек скатерти или полотенце. Она состоит из переплетенных нитей. Часть нитей идет, условно, слева направо, а часть – сверху вниз. Если скатерть повидала виды, то на ней есть зацепки, стяжки. Двумерное пространство с оператором Нийнехейса представляет собой что-то похожее – через каждую точку протянуты нити. В этом смысле теорема о расщеплении говорит, как локально устроено плетение нашей «скатерти», а изучение особых точек (теорема о линеаризации) – какие бывают простейшие узелки и зацепки.
На матрицу в нийенхейсовой геометрии тоже наложены некоторые условия, которые были открыты Альбертом Нийенхейсом еще в 50-х годах прошлого века. Несмотря на то, что этот объект был в распоряжении математиков последние 60 лет, он рассматривался как некий вспомогательный объект для решения других задач.
Похожая ситуация была с пуассоновой геометрией в 70-х годах прошлого века до тех пор, пока нескольким математикам не удалось заложить фундамент пуассоновой геометрии. Этот фундамент – некоторый набор базовых теорем, которые раскрывают богатство структуры и демонстрируют потенциал для ее изучения.
Одним из таких ученых был Алан Вайнштейн. Ему удалось доказать так называемую теорему о расщеплении и заложить основы линеаризации – обе эти математические идеи позже превратились в целые направления.
«В новых работах удалось получить похожие по глубине результаты – теорему о расщеплении для операторов Нийнехейса, а также сформулировать и в некоторых случаях решить проблему линеаризации. В этих же работах мы продемонстрировали глубокие связи полученных результатов с другими областями математики и математической физики», — говорит Коняев.

 Цивилизация
Цивилизация